|
Una de las rutinas que acabo de presentar a mi clase al comenzar el nuevo año durante las conversaciones matemáticas, es la rutina de verdadero o falso. Presento a mis estudiantes cuatro ecuaciones o comparaciones numéricas, explicando que algunas ecuaciones son verdaderas y otras falsas. Ellos tienen que averiguar cuál es cuál, utilizar un modelo y explicar su razonamiento. A medida que mis estudiantes se van sintiendo cómodos con la nueva rutina, empiezo a introducir nuevos elementos, como ecuaciones en ambos lados del símbolo de igual, u otros símbolos como los de mayor que (>) o menor que (<). En este punto algunos estudiantes pueden verse algo confusos, por lo que considero importante utilizar objetos para mostrar las comparaciones. En mi clase utilizo una zona con una mesa para situar dos vasitos de plástico transparente, cubos de base 10, y tarjetas borrables para escribir las ecuaciones. Pido a mis estudiantes que en cada vasito coloquen la cantidad de cubitos que dice la ecuación. Así de una manera visual pueden observar si la cantidad de un vasito es mayor, menor o igual que la cantidad de otro vasito, y por tanto discernir si el símbolo situado entre las dos ecuaciones es correcto o incorrecto. Una vez hecho el modelo físico, mis estudiantes dibujan el modelo con líneas de 10 y puntos, o con círculos en grupos de 5. Siempre trato de recalcar la importancia de hacer una representación organizada que les ayude a contar de una manera más fácil.
0 Comments
Con frecuencia encontramos que nuestros estudiantes, cuando se enfrentan a historias matemáticas o problemas con palabras, se sienten perdidos, no entienden lo que el problema les esta preguntando, y se enfocan solamente en los números que el problema presenta, lanzándose a resolver ecuaciones que ellos asumen son las correctas por razones que desconocemos. En otras ocasiones, nuestros estudiantes piensan que entienden el problema, y con frecuencia sacan conclusiones erróneas, sobre todo cuando se trata de resolver problemas de varios pasos. Una estrategia que podemos usar son los "problemas sin números". El objetivo es presentar problemas a los que se les ha quitado los números y presentarlos a nuestros estudiantes para hacerles reflexionar sobre la historia, invitarles a que se hagan preguntas, visualicen la situación que el problema presenta y después, paso a paso, introducir la información que necesitan para resolver ese problema. Para trabajar con problemas matemáticos sin números, sigue estos pasos:
|
AuthorHola! Soy Esther, bienvenid@ a este blog, en el que compartiré recursos educativos, curiosidades, reflexiones y otras cosillas. Gracias por tu visita. ArchivesCategories
All
|
||||||


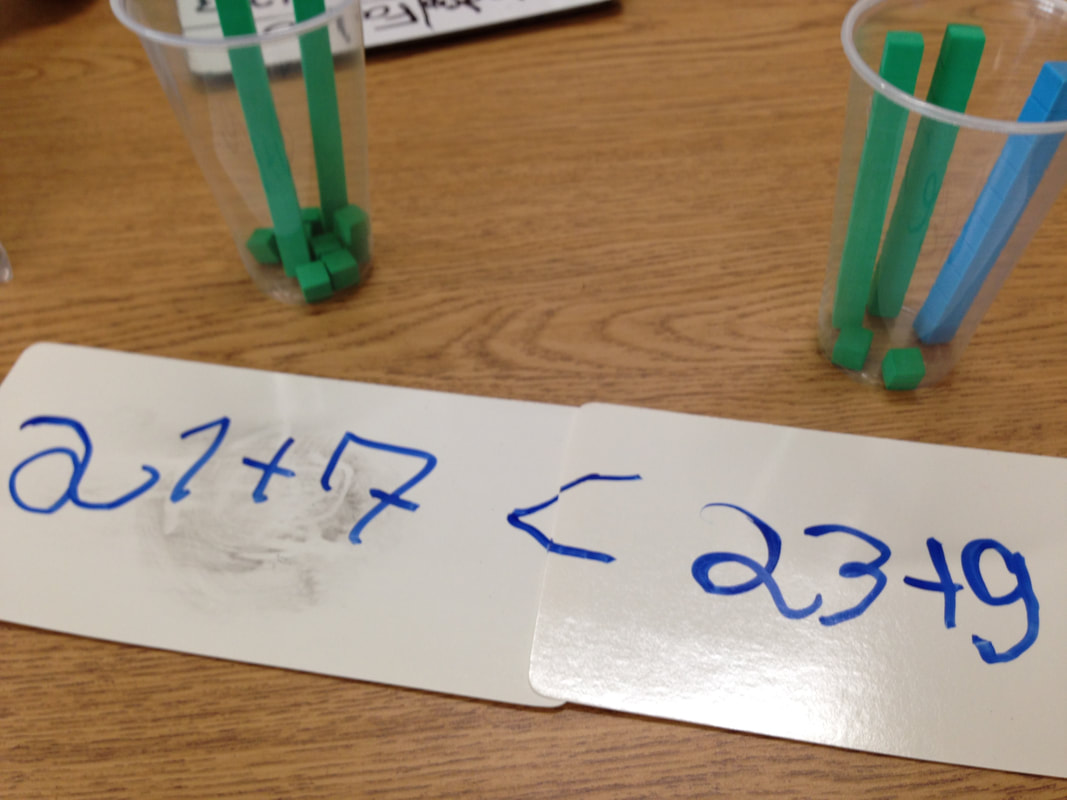
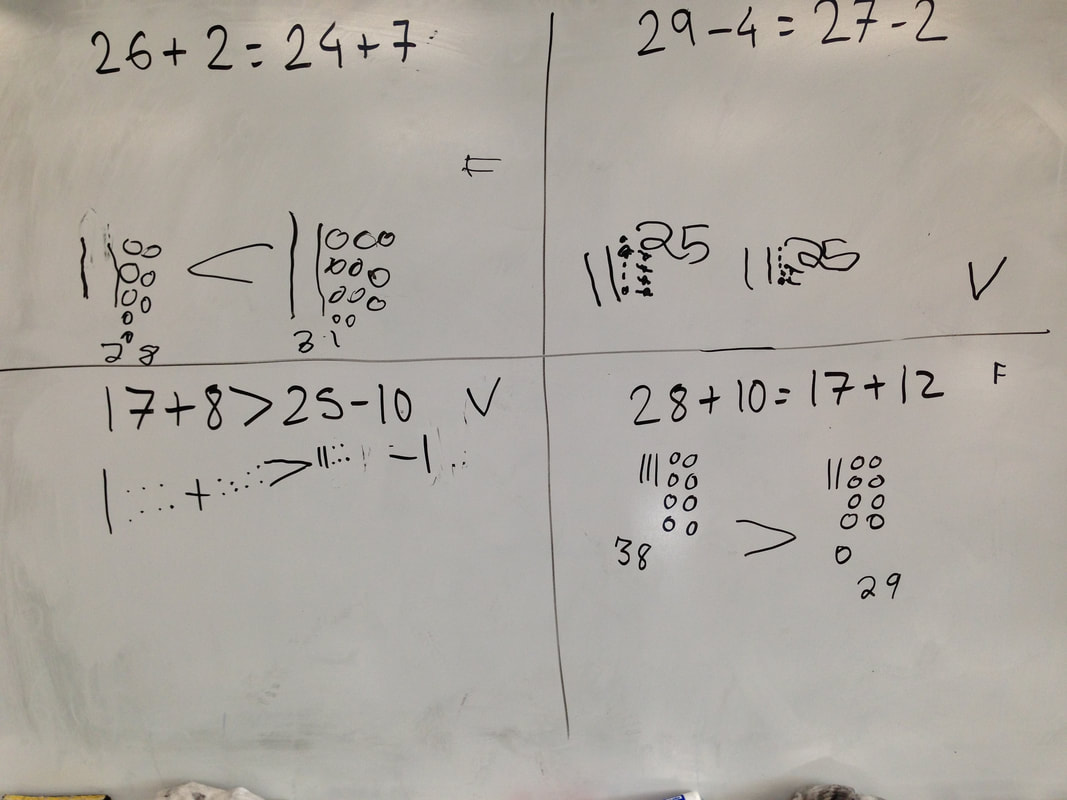
 RSS Feed
RSS Feed
